База Знаний: Функции Calc. LOGNORMDIST
LOGNORMDIST
Функция вычисляет значения для интегральной функции логнормального распределения.
Синтаксис функции:
| =LOGNORMDIST(x; μ; σ) |
|---|
где:
- x — вероятность, связанная с нормальным логарифмическим распределением;
- μ — среднее;
- σ — среднеквадратичное отклонение.
Переменная имеет логарифмически нормальное (логнормальное) распределение, если её натуральный логарифм имеет нормальное распределение. Параметры распределения — μ (среднее) и σ (среднеквадратичное отклонение).
Логнормальное распределение обычно используется для общего анализа надёжности, числа циклов до отказа при усталости, сопротивлении материалов и переменных нагрузках в вероятностном проектировании. Другое преимущество логнормального распределения состоит в том, что оно является положительно-определённым, таким образом оно часто полезно для представления параметров, которые не могут иметь отрицательных значений. Логнормальные распределения оказались полезными как распределения для количества осадков, для распределения размера частиц аэрозоля или капелек, и для многих других случаев.
Функция LOGNORMDIST вычисляет интегральную функцию плотности для логнормального распределения.
LOGNORMDIST(x; μ; σ) эквивалентно NORMDIST((LN(x) — μ)/σ; 0; 1; 1); она также может быть вычислена как 0,5 + 0,5 * ERF((LN(x) — μ)/(σ*SQRT(2)))
Функция LOGNORMDIST при x > 0 возвращает значение (1) и 0 в противном случае.
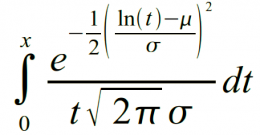
|
(1) |
| В разрабатываемом международном стандартном ODFF эта функция имеет дополнительный параметр, позволяющий также вычислять функцию плотности вероятности. |
InfraOffice.pro 3.1.x
