База Знаний: Функции Calc. PERCENTILE
PERCENTILE
Функция возвращает указанную процентиль[1] в списке чисел.
Синтаксис функции:
| =PERCENTILE(numberlist; fraction) |
|---|
где:
- numberlist — диапазон или массив чисел, не обязательно упорядоченный;
- fraction — значение процентили в интервале от 0 до 1 включительно.
Функция PERCENTILE возвращает значение ниже которого лежат fraction чисел из numberlist.
Функция PERCENTILE внутренне назначает разряд каждому числу в numberlist, где 0 — разряд самого наименьшего числа, 1 — следующее из самых наименьших чисел и так далее. Разряд r значения, которое будет найдено — fraction * (N – 1), где N — количество чисел в numberlist. Если r — целое число, возвращена соответствующее значение из numberlist; в противном случае значение вычисляется пропорционально между значениями с разрядом |r| и |r| + 1.
Эта функция может быть полезной, например, для определения оценки, ниже которой лежит определённый процент из всех оценок теста. Она имеет ограниченное использование с небольшим списком чисел.
Функция PERCENTILE возвращает максимум, медиану, минимальное значение когда fraction — 1, 0,5 и 0 соответственно.
PERCENTILE(A2:A99; 0.6)
Ячейки, A2:A99 содержат массив оценок теста, формула возвращает оценку, ниже которой лежат 60% массива.
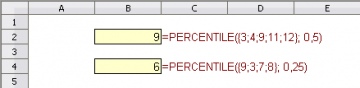
На рис. 1 два примера иллюстрируют вычисление, но не предназначены для отображения практического применения:
- в ячейке B2 возвращается 9, медиана списка;
- в ячейке B4 возвращается 6. В списке есть 4 числа. Разряд значения, которое будет найдено — 0,25 * (4 – 1) = 0,75. Самому малому числу 3 назначен разряд 0; следующему большему числу 7 назначен разряд 1. Значение с разрядом 0,75 лежит между 3 и 7, и вычисляется как 3 + (7 – 3) * 0,75 = 6.
InfraOffice.pro 3.1.x
- ↑ Процентиль — мера расположения данных выборки или распределения. Говорят, что n-й процентиль — это такое значение, ниже которого расположено n процентов наблюдений данной переменной. Следовательно, 40-й процентиль — это значение, ниже которого расположено 40% результатов наблюдений; 50-й процентиль называется медианой, а 25-й и 75-й процентили — нижним и верхним квартилями соответственно.