Difference between revisions of "RU/kb/00000686"
From Wiki
Jump to navigationJump to search (Основной текст) |
|||
| Line 16: | Line 16: | ||
* ''n'' — значение в интервале между ''a'' и ''b'', для которого вычисляется функция; | * ''n'' — значение в интервале между ''a'' и ''b'', для которого вычисляется функция; | ||
* ''α'' и ''β'' — параметры распределения; | * ''α'' и ''β'' — параметры распределения; | ||
| − | * ''a'' — необязательная нижняя граница интервала изменения n (по умолчанию, если опущена, равна 0); | + | * ''a'' — необязательная нижняя граница интервала изменения ''n'' (по умолчанию, если опущена, равна 0); |
| − | * ''b'' — необязательная верхняя граница интервала изменения n (по умолчанию, если опущена, равна 1). | + | * ''b'' — необязательная верхняя граница интервала изменения ''n'' (по умолчанию, если опущена, равна 1). |
Revision as of 12:47, 4 February 2012
< Энциклопедия | База знаний | Модули OpenOffice.org | Calc | Справочник функций | Статистические функции
BETADIST
Функция вычисляет интегральную функцию бета-распределения[1]
Синтаксис функции:
| =BETADIST(n; α; β; a; b) |
|---|
где:
- n — значение в интервале между a и b, для которого вычисляется функция;
- α и β — параметры распределения;
- a — необязательная нижняя граница интервала изменения n (по умолчанию, если опущена, равна 0);
- b — необязательная верхняя граница интервала изменения n (по умолчанию, если опущена, равна 1).
Бета распределение — семейство непрерывных распределений вероятности, определённых для интервала от a до b, где α и β — параметры, управляющие формой распределения, а n находится между a и b.
Функция BETADIST для n >= a и n <= b вычисляет интегральную функцию распределения (1).
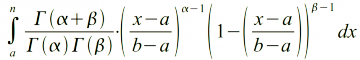
|
(1) |
InfraOffice.pro 3.1.x
- ↑ Бета распределение в теории вероятностей и статистике — двухпараметрическое семейство абсолютно непрерывных распределений.
