Difference between revisions of "RU/kb/00000743"
From Wiki
Jump to navigationJump to search (Основной текст) |
|||
| Line 6: | Line 6: | ||
<section begin=toc /> | <section begin=toc /> | ||
=== SLOPE === | === SLOPE === | ||
| − | Функция подбирает прямую линию к данным, используя линейную регрессию и возвращает его наклон. | + | <section begin=description />Функция подбирает прямую линию к данным, используя линейную регрессию и возвращает его наклон.<section end=description /> |
==== Синтаксис функции: ==== | ==== Синтаксис функции: ==== | ||
Latest revision as of 12:35, 13 March 2012
< Энциклопедия | База знаний | Модули OpenOffice.org | Calc | Справочник функций | Статистические функции
SLOPE
Функция подбирает прямую линию к данным, используя линейную регрессию и возвращает его наклон.
Синтаксис функции:
| =SLOPE(yvalues; xvalues) |
|---|
где:
- yvalues; xvalues — одностроковые или одностолбцовые диапазоны, определяющие точки в наборе данных.
Диапазоны yvalues и xvalues должны быть одинакового размера.
Функция SLOPE подбирает прямую линию через эти точки данных, используя метод линейной регрессии (наименьших квадратов[1]). После чего она возвращает наклон этой линии.
Уравнение прямой линии можно задать как y = a + bx. Метод линейной регрессии вычисляет (1) и (2) b — наклон, возвращаемый этой функцией.
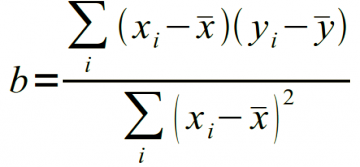
|
(1) |
| (2) |
Параметры xvalues и yvalues всегда оцениваются как формулы массива.
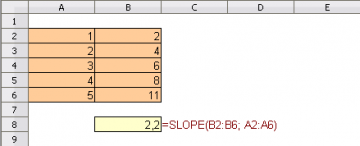
На рис. 1:
- в ячейке B8 возвращается 2,2. Уравнение найденной прямой линии — почти соответствует y = 2x — таким образом, наклон — почти (но не совсем) 2.
InfraOffice.pro 3.1.x
- ↑ Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.