Difference between revisions of "RU/kb/00000684"
From Wiki
Jump to navigationJump to search (Основной текст) |
|||
| Line 6: | Line 6: | ||
<section begin=toc /> | <section begin=toc /> | ||
=== B === | === B === | ||
| − | Функция вычисляет вероятности для биномиального распределения<ref>''Биномиальное распределение'' — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна ''p''.</ref>. | + | <section begin=description />Функция вычисляет вероятности для биномиального распределения<ref>''Биномиальное распределение'' — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна ''p''.</ref>.<section end=description /> |
==== Синтаксис функции: ==== | ==== Синтаксис функции: ==== | ||
Revision as of 10:13, 13 March 2012
< Энциклопедия | База знаний | Модули OpenOffice.org | Calc | Справочник функций | Статистические функции
B
Функция вычисляет вероятности для биномиального распределения[1].
Синтаксис функции:
| =B(n; p; k; k2) |
|---|
где:
- n — число независимых случайных экспериментов;
- p — вероятность «успеха» в каждом из случайных экспериментов;
- k; k2 — нижний и верхний пределы диапазона распределения для n независимых случайных экспериментов, k2 = k если k2 опущен.
Для n независимых случайных экспериментов, каждый с вероятностью успеха p, функция B возвращает вероятность того, что число успехов будет между k и k2 включительно, или если k2 опущен, вероятность того, что число успехов будет точно k.
Вероятность вычисляется как (1), где k2 = k если k2 опущен.
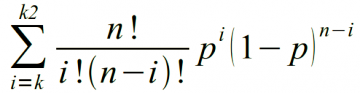
|
(1) |
На рис. 1:
- в ячейке B2 возвращается приблизительно 0,29 (29%), вероятность того, что номер четыре будет выброшен точно два раза за 10 бросков игральной кости.
InfraOffice.pro 3.1.x
- ↑ Биномиальное распределение — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна p.
