Difference between revisions of "RU/kb/00000461"
From Wiki
Jump to navigationJump to search (Основной текст) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 6: | Line 6: | ||
<section begin=toc /> | <section begin=toc /> | ||
=== BESSELY === | === BESSELY === | ||
| + | <section begin=description /> | ||
Функция вычисляет функцию Бесселя второго рода (функцию Неймана или Вебера). | Функция вычисляет функцию Бесселя второго рода (функцию Неймана или Вебера). | ||
| + | <section end=description /> | ||
==== Синтаксис функции: ==== | ==== Синтаксис функции: ==== | ||
| Line 28: | Line 30: | ||
| (2) | | (2) | ||
|- | |- | ||
| − | |[[File:Function_BESSELY_formula.png| | + | |[[File:Function_BESSELY_formula.png|400px]] |
| (3) | | (3) | ||
|} | |} | ||
Latest revision as of 18:16, 12 March 2012
< Энциклопедия | База знаний | Модули OpenOffice.org | Calc | Справочник функций | Математические функции
BESSELY
Функция вычисляет функцию Бесселя второго рода (функцию Неймана или Вебера).
Синтаксис функции:
| =BESSELY(x; n) |
|---|
где:
- x — значение, для которого вычисляется функция;
- n — порядок функции Бесселя.
Функция BESSELY возвращает функцию Бесселя второго рода, n-ого порядка от переменной x. Функции Бесселя второго рода (1), (также известные как функции Неймана (2) или Вебера) — решения дифференциального уравнения Бесселя, бесконечные в точке x = 0.
| (1) | |
| (2) | |
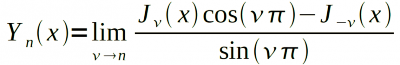
|
(3) |
InfraOffice.pro 3.1.x
