Difference between revisions of "RU/kb/00000759"
From Wiki
Jump to navigationJump to search (Основной текст) |
|||
| Line 7: | Line 7: | ||
<section begin=toc /> | <section begin=toc /> | ||
=== WEIBULL === | === WEIBULL === | ||
| − | Функция вычисляет значения для распределения Вейбулла. | + | <section begin=description />Функция вычисляет значения для распределения Вейбулла.<section end=description /> |
==== Синтаксис функции: ==== | ==== Синтаксис функции: ==== | ||
Latest revision as of 12:40, 13 March 2012
< Энциклопедия | База знаний | Модули OpenOffice.org | Calc | Справочник функций | Статистические функции
WEIBULL
Функция вычисляет значения для распределения Вейбулла.
Синтаксис функции:
| =WEIBULL(x; k; λ; mode) |
|---|
где:
- x — значение, для которого вычисляется вероятность, x >= 0;
- k — параметр распределения (коэффициент формы);
- λ — параметр распределения (коэффициент масштаба);
- mode — логическое значение, определяющее форму возвращаемого распределения вероятностей.
Распределение Вейбулла — непрерывное распределение вероятности, с параметрами k > 0 (форма) и λ > 0 (масштаб). Этому распределению хорошо подчиняется распределение отказов в объектах, содержащих большое количество однотипных неремонтируемых элементов (полупроводниковых приборов, микромодулей и т. д.). Названо в честь шведского инженера Валодди Вейбулла (Waloddi Weibull, 1887—1979 гг.).
Если mode = 1, функция WEIBULL вычисляет плотность вероятности распределения Вейбулла (1).
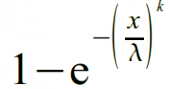
Если mode = 0, функция WEIBULL вычисляет совокупную функцию распределения для распределения Вейбулла (2).
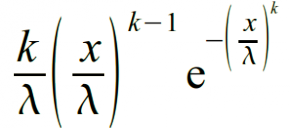
|
(1) |
|
(2) |
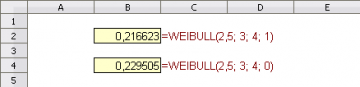
На рис. 1:
- в ячейке B2 возвращается приблизительно 0,216623, значение функции плотности вероятности с k = 3 и λ = 4 для x = 2,5;
- в ячейке B4 возвращается приблизительно 0,229505, значение функции интегрального распределения с k = 3 и λ = 4 для x = 2,5.
InfraOffice.pro 3.1.x